systems/processes/elements of Tao

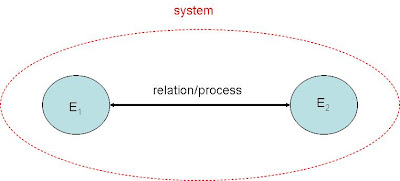
A system generally includes at least two elements of the system (E1, E2) and a relation or process between them:

The elements items can be anything, from elementary particles to molecules to physiological organs to people who interact each others to mathematical laws. Sometimes we are familiar with the elements of the system, but we know little or nothing about their relationships; conversely often we know the process but do not know what are the elements that are implementing it and how they work.

In the previous figure the relationship between the elements is unique/one-way. This means that E1 has influence to E2 but not vice versa, or has influence but do not know or do not care about, for example in the Sun-Earth system.

The relation/process can be bijective/bidirectional, i.e. each element of the system interacts with the other:

The definition of a system is based on the cognitive logic competence to define a reasonable set. As such, a system always refers to an observer that defines a context or vice versa, a context which defines an observer:

As such, the definition of a system is always relative and subjective.
A general representation of a system may be:

Systems and their Representation
Graphics created by Marshall Clemens, NECSI